1. Prozent als Verhältnis
Wenn Sie zwei Zahlen dividieren, entsteht ein Verhältnis. Ein Verhältnis ist die Antwort auf die Frage: „Wie viel ist die eine Zahl im Vergleich zur anderen.“ Am besten, Sie sehen sich das Ganze an.
Wörter 1
das Verhältnis, die Nuss, knacken, die Grundlage, frei, der Parkplatz, die Hälfte, Frankreich, finden, herausfinden, überhaupt, wovon, nämlich, der Grund, der Wert, der Grundwert, finden, googeln, schnell, leicht, dividieren, klein/kleiner/am kleinsten, der Fall, der Taschenrechner, runden, der Name, das Wort, das Hundertstel, die Stelle, verstecken, die Aufgabe, rechnen, berechnen, das Foto, geben, reingeben/hineingeben, der Moment, brauchen, die Anzahl, die Zahl, veranschaulichen, das Ganze, der Satz, der Prozentsatz, belegen/belegt, der Anteil
Übungen
Wörter 2
der Strich, die Butter, der Teil, gleich, bereits, brauchen, verbrauchen, mittlerweile, nun, ändern, sehen, aussehen, googeln, das Fahrrad, billig/billiger/am billigsten, verbilligt, neu, alt, der Preis, der Ausgang, der Ausgangspreis, tatsächlich, der Schuh, das Kind, die Kinderschuhe, tragen, betragen, der Nachlass, das Paar, die Reihenfolge, annehmen, das Verhältnis, der Normalpreis, ergänzen, die Angabe, die Prozentangabe, die Flasche, das Wasser, das Mineral, das Mineralwasser, die Mineralwasserflasche, der Stoff, das Material, künstlich, der Kunststoff, das Recyclat, verwenden, wieder, wiederverwenden, vegan, gesamt, der Inhalt, produzieren, tierisch, das Produkt
Butter
Die Striche kennzeichnen gleiche Teile. Wie viel Prozent der Butter wurden bereits verbraucht?


Lösung
Noch einmal Parken
Wir befinden uns in Bordeaux. Mittlerweile haben sich die freien Parkplätze des ersten Beispiels geändert. Wie viel Prozent sind nun frei? Wie sieht es mit den weiteren zwei Parkplätzen aus? Hier müssten Sie selbst googeln.
Fahrrad
Das Fahrrad ist billiger. Um wie viel Prozent würde es verbilligt?
Lösung
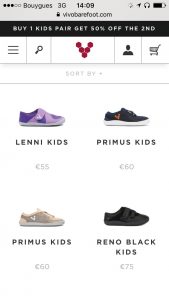
Kinderschuhe
Wenn Sie ein Paar Kinderschuhe kaufen, dann bekommen Sie ein zweites Paar um 50% billiger. Sie machen das und kaufen tatsächlich zwei Paar. Wie viel Prozent beträgt der Nachlass?
Lösung
Mineralwasser
Was bedeuten die Prozentangaben auf dieser Mineralwasserflasche?
Lösung
2. Prozent als Vorhersage
Wenn Sie wissen, dass ein Prozentsatz einer Menge eine Eigenschaft hat, dann können Sie das auch auf andere Mengen anwenden.
Wörter 3
wissen, der Satz, der Prozentsatz, die Menge, die Eigenschaft, anwenden, die Anwendung, die Brille, tragen, der Brillenträger, der Mensch, unter
Beispiel
30% der Menschen sind Brillenträger. Wie viele Brillenträger sind unter 1000 Menschen?
30% = 0,03
0,30 • 1000 = 300
Antwort: Unter 1000 Menschen sind 300 Brillenträger.
Übungen
Berechnen Sie bitte 12% von 3500, 45% von 700.000, 80% von 375 und 5% von 900.
Lösungen
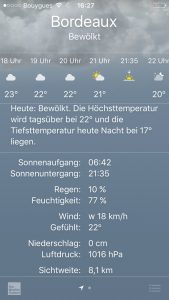
Wettervorhersage
Regen 10% bedeutet: An 100 Tagen mit der selben Wettersituation wird es an 10 regnen.
Wörter 4
sagen, vorher, vorhersagen, das Wetter, die Wettervorhersage, regnen, der Regen, der Tag, die Situation, die Wettersituation, dieselbe, die Angabe, die Prozentangabe, die Feuchtigkeit, die Luft, die Luftfeuchtigkeit, das Wasser, unsichtbar, der Dampf, der Wasserdampf, spüren, maximal, die Menge, bedeuten, schon
Wenn Sie genau schauen, sehen Sie noch eine zweite Prozentangabe in der Wettervorhersage: 75% Luftfeuchtigkeit. Wenn Wasser in der Luft ist, dann sehen wir das nicht. Wasserdampf ist unsichtbar. Wir spüren es aber. 100% ist die maximale Menge an Wasser, die in der Luft sein kann. 75% bedeutet, dass schon viel Wasser in der Luft ist.
Übung
Was bedeutet die Prozentangabe in diesem Wetterbericht?
Lösung
3. Prozent beim Kaufen und Verkaufen
Wörter 5
kaufen, verkaufen, der Händler, die Ware, davon, abführen, die Steuer, der Umsatz, die Umsatzsteuer, das Amt, die Finanzen, das Finanzamt, der Betrag, kosten, erhalten, der Rabatt, die Leistung, der Dienst, die Dienstleistung, ursprünglich
Tipp
Wenn eine Ware mit 20% Umsatzsteuer einen Betrag kostet, dann bezahlen Sie dafür 120%: für die Ware bezahlen Sie 100% und für die Umsatzsteuer 20%. Um aus dem Gesamtbetrag den Betrag ohne Umsatzsteuer zu berechnen, müssen Sie zuerst durch 120 dividieren, um 1% zu erhalten, und dann mit 100 multiplizieren, um 100% zu erhalten.
Wenn eine Ware mit 25% Rabatt einen Betrag kostet, dann bezahlen Sie dafür 75%. Um aus dem bezahlten Betrag den Betrag ohne Rabatt zu berechnen, müssen Sie zuerst durch 75 dividieren, um 1% zu erhalten, und dann mit 100 multiplizieren, um 100% zu erhalten.
Übungen
Umsatzsteuer 1
Sie verkaufen als Händler eine Ware um 800 € und müssen davon 20% Umsatzsteuer an das Finanzamt abführen. Wie viele € sind das? Wie groß ist der Preis ohne Umsatzsteuer?
Lösung
Umsatzsteuer 2
Sie verkaufen eine Dienstleistung um 150 € und müssen davon 10% Umsatzsteuer an das Finanzamt abführen. Wie viele € sind das? Wie groß ist der Preis ohne Umsatzsteuer?
Lösung
Abzug 1
Ein Produkt kostet nach Abzug eines 25% Rabattes 60 €. Wie hoch war der ursprüngliche Preis?
Lösung
Abzug 2
Ein Produkt kostet 300 €. 5% Rabatt wird abgezogen. Wie viel kostet die Ware abzüglich des Rabatts?
Lösung
4. Häufige Prozentanteile
Das lernen Sie am besten auswendig:
100% – das Ganze
75% – drei Viertel
67% – zwei Drittel
50% – die Hälfte
33% – ein Drittel
25% – ein Viertel
12,5% – ein Achtel
10% – ein Zehntel
1% – ein Hundertstel
5. Das wars’s für dieses Mal
Wörter 6
sagen, die Grundlage, der Rest, schauen, hinschauen, probieren, ausprobieren, die Sicherheit, gewinnen, das Zeichen, das Prozentzeichen, der Freund, erleichtern, verstehen, vergleichen
Schön, dass Sie beim Sommerkurs dabei sind. Es gäbe sicher noch viel zu sagen, was Prozente betrifft. Aber die Grundlagen haben Sie kennen gelernt, der Rest ist hinschauen, ausprobieren, Sicherheit gewinnen. Prozentzeichen sind unsere Freunde. Sie erleichtern uns Zahlen zu verstehen und zu vergleichen.
Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!