
Diese Tafel ist ein Rechteck. Sie ist rechteckig.
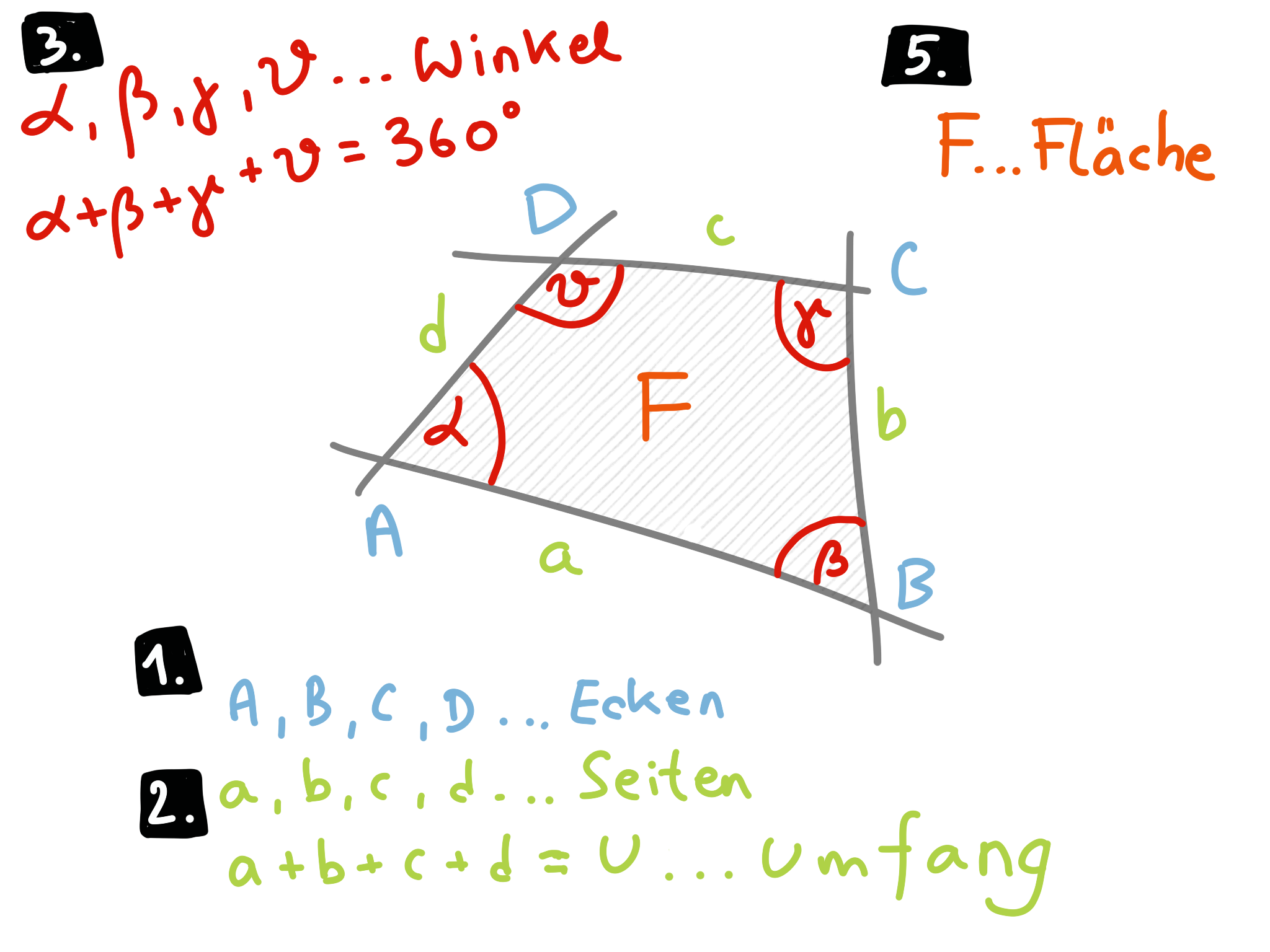
1. Grundbegriffe
In diesem Kapitel geht es weniger um komplizierte Berechnungen. Es geht mehr darum, die Begriffe richtig zu verwenden. Das wollen wir jetzt üben.
Wörter 1
wenig/weniger/am wenigsten, kompliziert, rechnen, die Berechnung, der Begriff, verwenden, üben, zeichnen, die Zeichnung, die Ecke, das Dreieck, das Viereck, nennen, benennen, das Element, die Tafel, das Rechteck, rechteckig, dreieckig, die Seite, die Ecke, der Winkel, schließen, einschließen, der Umfang, die Summe, die Länge, die Fläche, das Gebiet, die Formel, die Regel, der Punkt, der Eckpunkt, der Großbuchstabe, der Kleinbuchstabe, der griechische Buchstabe, zeichnen, bezeichnen, die Verwirrung
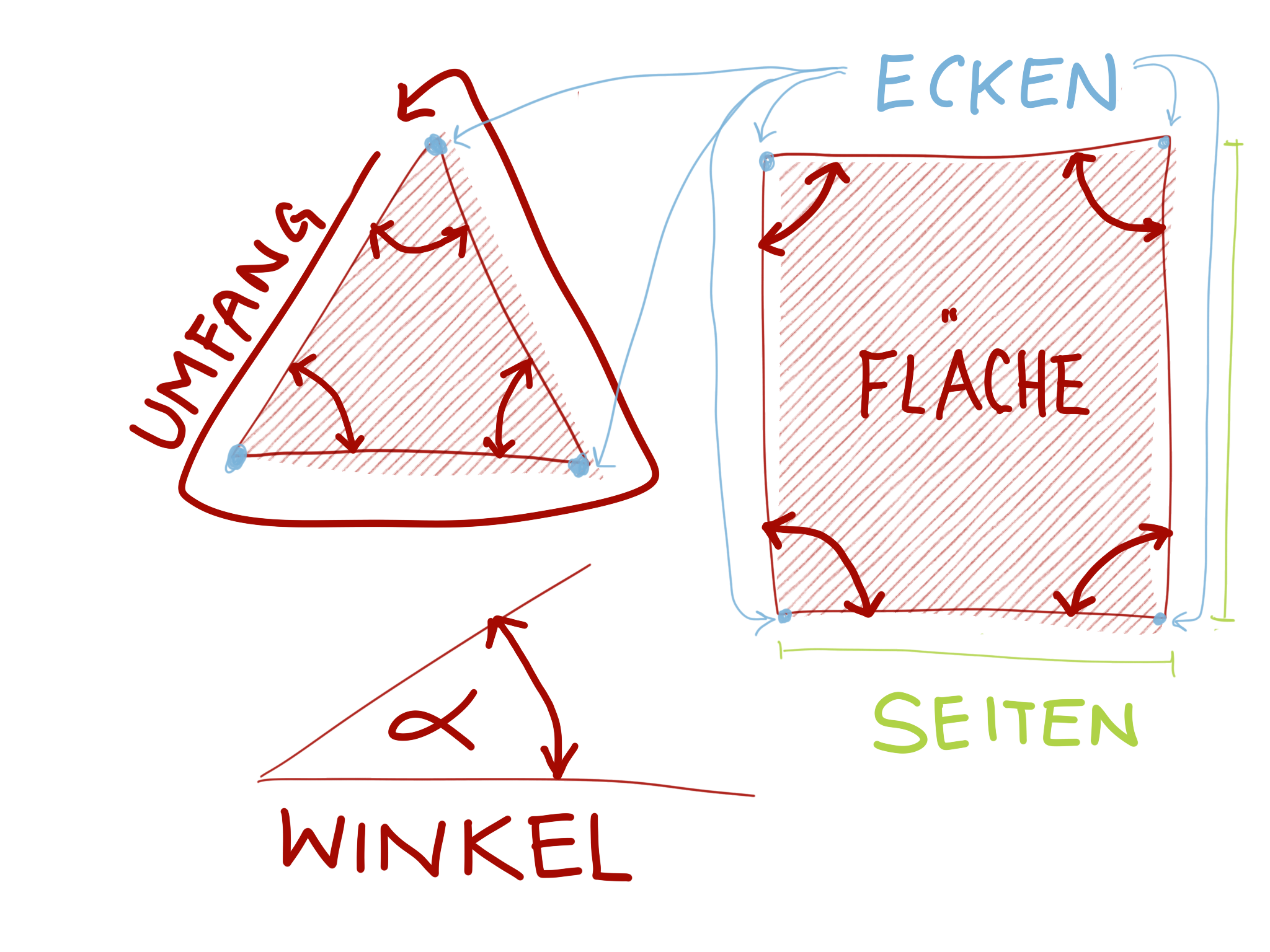
Dreiecke haben drei Seiten, drei Ecken/Eckpunkte und drei eingeschlossene Winkel. Vierecke haben vier Seiten, vier Ecken/Eckpunkte und vier eingeschlossene Winkel.
Der Umfang ist die Summe der Länge der Seiten. Die Fläche ist der Inhalt des Gebietes, das die Seiten einschließen. Oft gibt es eine Formel, mit der wir die Fläche berechnen können. Oft gibt es eine einfache Regel.
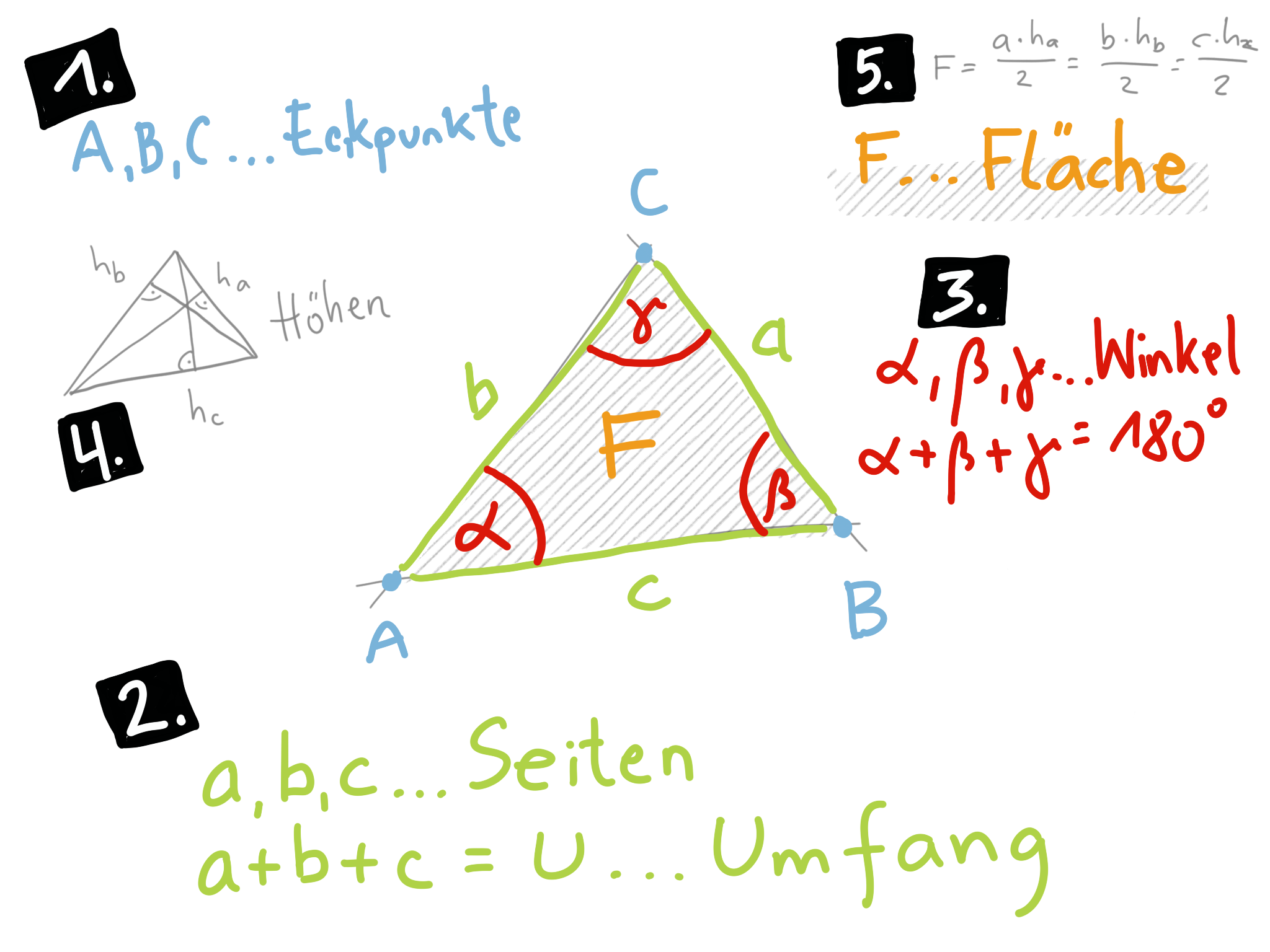
Die Eckpunkte bezeichnen wir mit Großbuchstaben. Die Seiten bezeichnen wir mit Kleinbuchstaben. Die Winkel bezeichnen wir mit griechischen Buchstaben. So gibt es keine Verwirrung.
2. Dreiecke
Wörter 2
das Dreieck, die Eigenschaft, besonders, der Name, eigen, gleich, gleichseitig, lange, der Winkel, das Grad, der Schenkel, gleichschenkelig, die Höhe, senkrecht, stehen, einzigartig, beginnen, der Mittelpunkt, rechtwinkelig, unterschiedlich, das Verhältnis, der Lehrsatz, Pythagoras, lernen, kennenlernen, allgemein, unterschiedlich, besonders, die Regelmäßigkeit, brauchen, die Skizze
Manche Dreiecke haben besondere Eigenschaften. Sie bekommen eigene Namen.
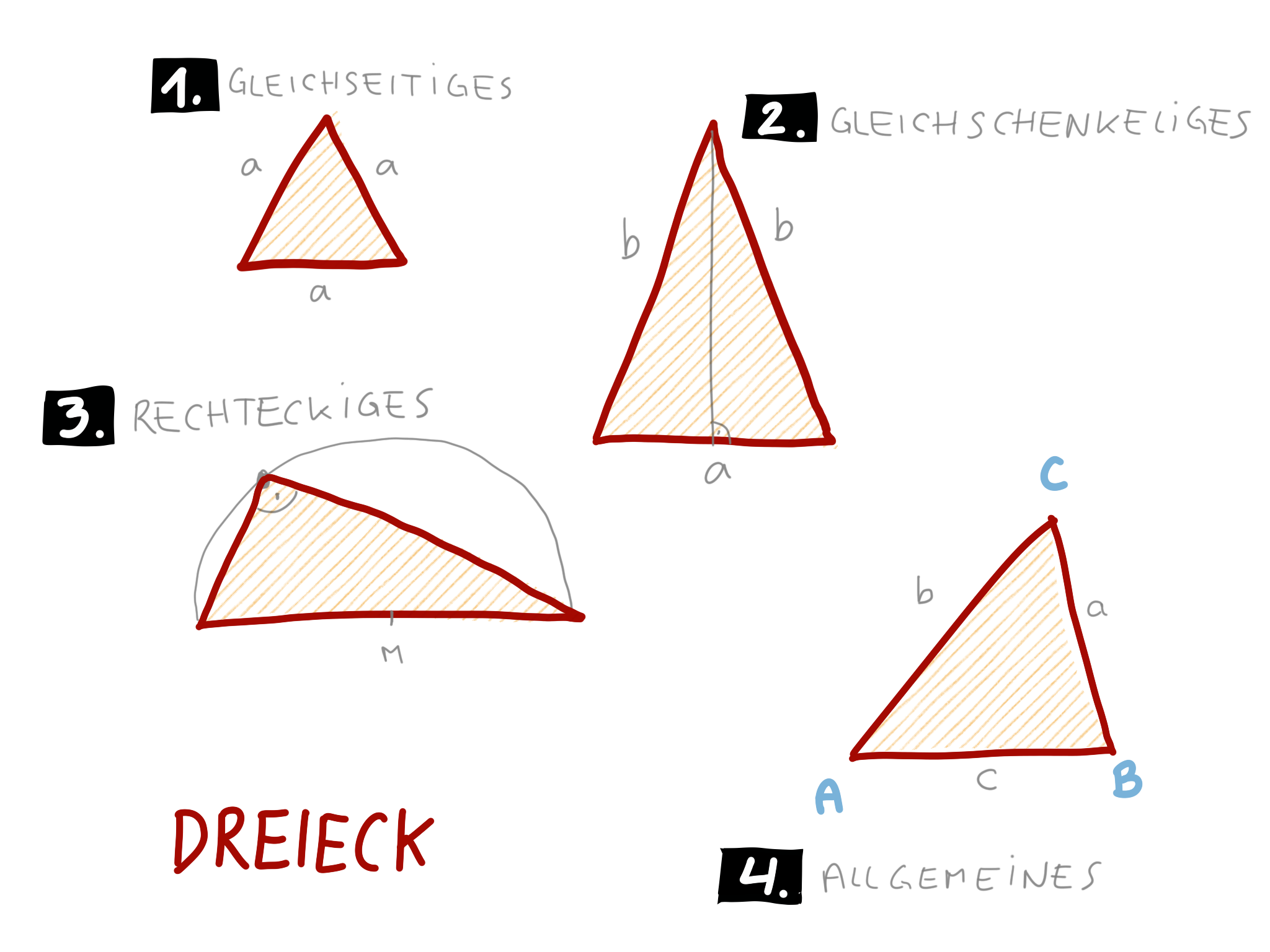
(1) Das gleichseitige Dreieck hat drei gleich lange Seiten. Jeder Winkel ist gleich groß, nämlich 180 Grad : 3 = 60 Grad.
(2) Das gleichschenkelige Dreieck hat zwei gleich lange Seiten. Die Höhe steht senkrecht auf die einzigartige Seite. Sie beginnt in ihrem Mittelpunkt. Es gibt zwei gleiche Winkel und einen dritten anderen Winkel.
(3) Das rechtwinkelige Dreieck hat einen Winkel mit 90 Grad. Die Seiten sind unterschiedlich lang. Sie stehen aber in einem Verhältnis, das besonders schön und einfach ist. Wir werden dieses Verhältnis später als „Lehrsatz des Pythagoras“ kennenlernen. Die Fläche ist besonders einfach zu berechnen, weil ein rechtwinkeliges Dreieck ein halbes Rechteck ist.
(4) Das allgemeine Dreieck hat unterschiedliche Seiten und Winkel. Es gibt keine besonderen Regelmäßigkeiten. Um ihre Flächen auszurechnen, brauchen wir eine Seite und ihre Höhe. Eine Höhe steht senkrecht auf eine Seite und geht durch den Eckpunkt, der gegenüberliegt. Wie das aussieht, sehen wir in der folgenden Skizze in Punkt 4.
3. Vierecke
Wörter 3
das Viereck, die Eigenschaft, der Name, die Formel, der Umfang, die Fläche, die Sammlung, die Formelsammlung, wichtig/wichtiger/am wichtigsten, stellen, zusammenstellen, vergleichen, der Text, die Skizze, das Quadrat, senkrecht, die Diagonale, halbieren, gegenüber, liegen, gegenüberliegend, parallel, die Raute, schief, das Rechteck, die Länge, die Breite, das Parallelogramm, das Trapez, das Deltoid, fehlen, lang/lange, ändern, ständig
Manche Vierecke haben besondere Eigenschaften. Sie bekommen eigene Namen. Formeln für Umfang und Fläche finden Sie in Ihrer/einer Formelsammlung. Wir haben hier die wichtigsten Eigenschaften zusammengestellt. Wir möchten sie kennen. Vergleichen Sie dazu den Text unten mit den Skizzen.
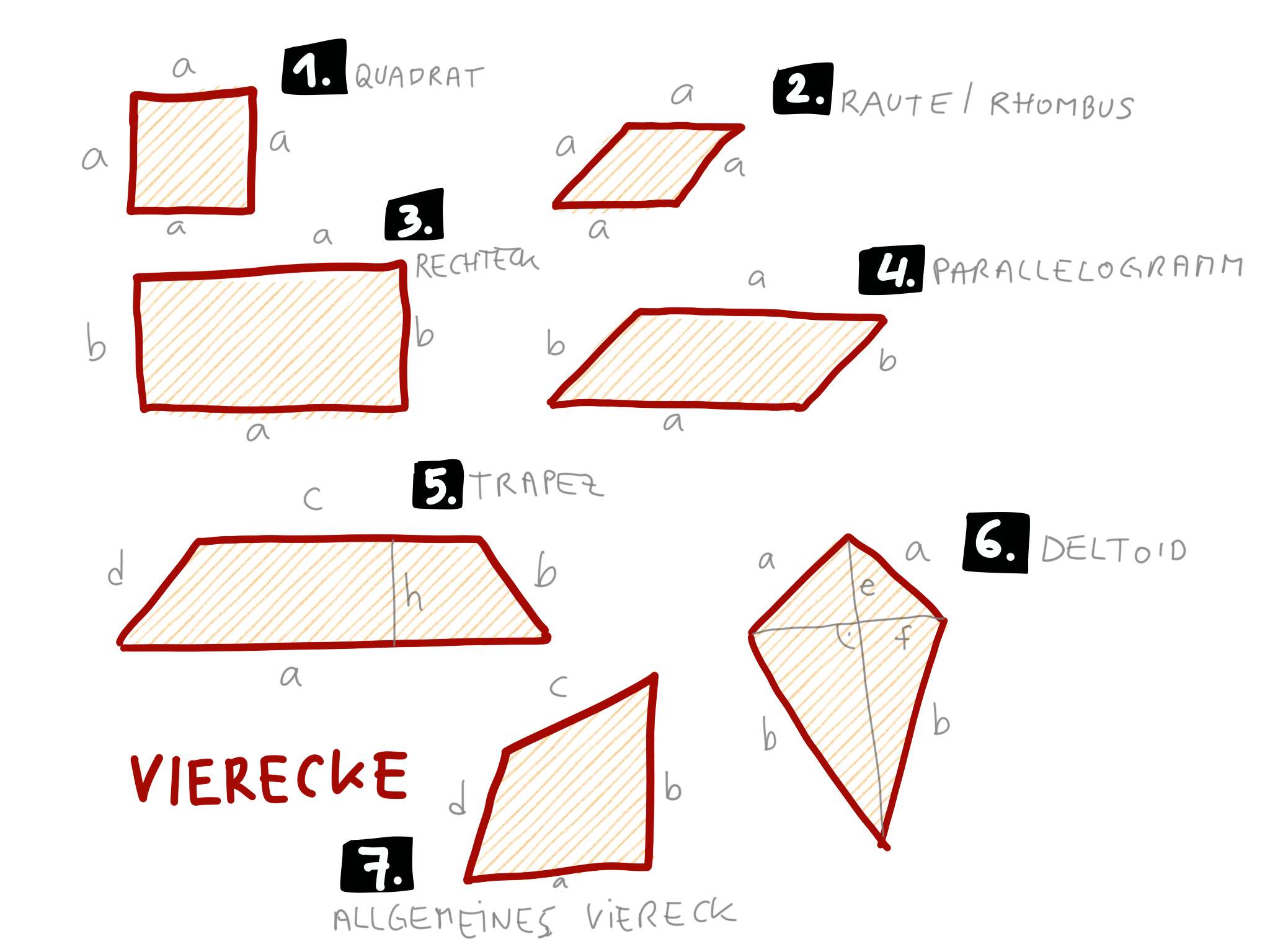
(1) Das Quadrat hat vier gleich lange Seiten. Sein Umfang ist leicht zu berechnen: 4-mal die Länge der Seite. Seine Fläche ist Seite mal Seite. Die Winkel sind gleich groß: 360 Grad : 4 = 90 Grad. Das ist senkrecht. Die Seiten stehen senkrecht aufeinander. Auch die Diagonalen stehen senkrecht. Sie halbieren einander. Gegenüberliegende Seiten sind parallel.
(2) Die Raute ist ein Quadrat, das schief geworden ist. Die Diagonalen stehen senkrecht. Sie halbieren einander. Gegenüberliegende Seiten sind parallel.
(3) Das Rechteck hat eine Länge a und eine Breite b. Die Seiten stehen senkrecht aufeinander. Die Diagonalen sind nicht mehr senkrecht. Sie halbieren aber einander. Der Umfang ist leicht zu berechnen: 2a + 2b. Auch die Fläche ist leicht zu berechnen: a • b. Gegenüberliegende Seiten sind parallel.
(4) Das Parallelogramm ist ein Rechteck, das schief geworden ist. Die Diagonalen halbieren einander. Gegenüberliegende Seiten sind parallel.
(5) Das Trapez hat zwei Seiten, die parallel sind.
(6) Das Deltoid hat zweimal zwei gleich lange Seiten. Die Diagonalen sind unterschiedlich lang. Sie stehen senkrecht aufeinander.
In dieser Skizze fehlt der Punkt (4). Wir haben damit beim Dreieck die Höhen bezeichnet. Beim allgemeinen Viereck gibt es keine eindeutige Höhe. Sie ändert sich ständig.
Frage
Was sind das für geometrische Figuren?

Klettergerüst am Spielplatz
Lösung
4. Grundlegende Konstruktionsaufgaben
Wörter 5
grundlegend, die Aufgabe, konstruieren, die Konstruktion, zeichnen, messen, fehlen, berechnen, finden
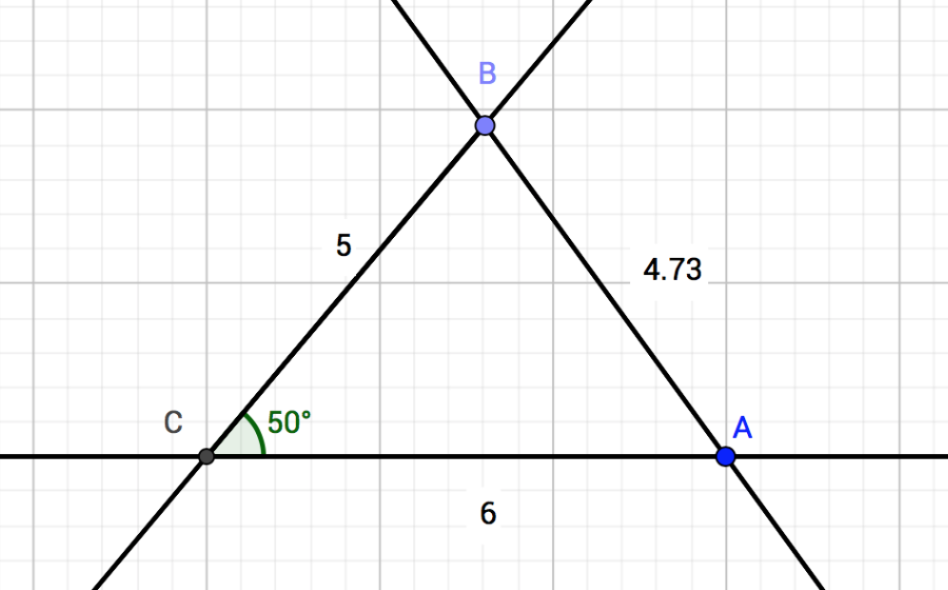
Zeichnen Sie ein Dreieck mit a = 6 cm, b = 5cm und γ = 50°. Messen Sie die fehlenden Seiten und Winkel, und berechnen Sie den Umfang.
Lösung
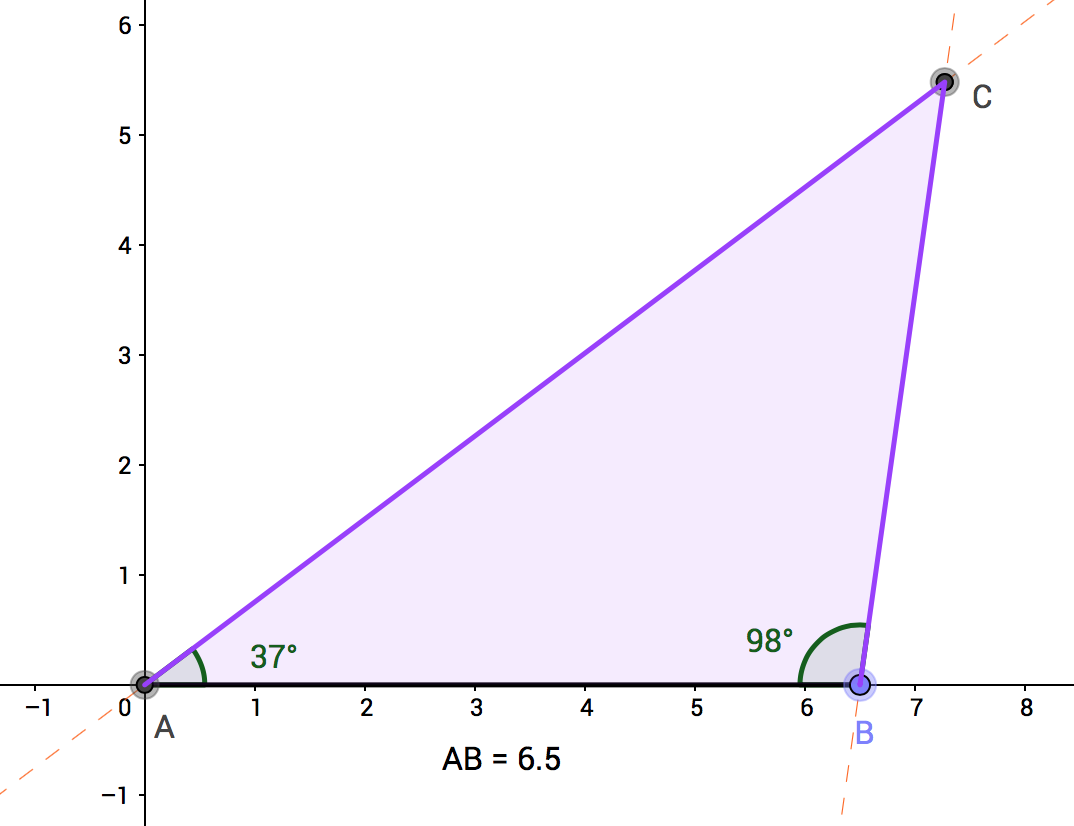
Zeichnen Sie ein Dreieck mit c = 6,5 cm, α = 37° und β = 98°.
Lösung
5. Erweiterte Konstruktionsaufgaben
Wörter 6
die Koordinaten, geben, gegeben, zeichnen, rechtwinkelig, das Koordinatensystem, konstruieren, die Symmetrale, die Strecke, die Streckensymmetrale, die Mitte, die Senkrechte, die Mittelsenkrechte, die Gerade, kennen, erkennen, das Dreieck, gleichschenkelig, spiegeln, kurz/kürzer/am kürzesten, die Entfernung, die Achse, die Spiegelachse, dynamisch
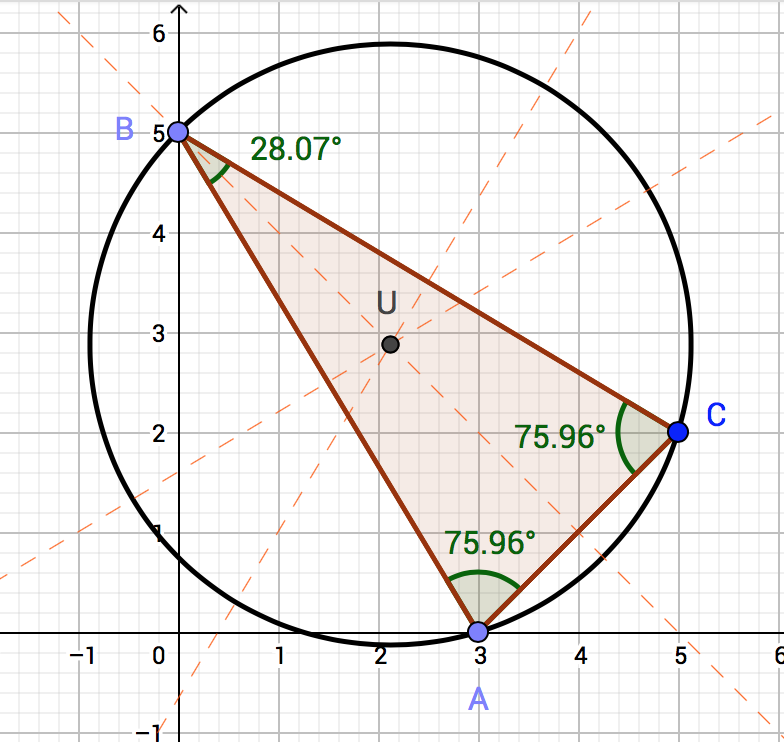
Das Dreieck ABC ist durch die Koordinaten der Eckpunkte gegeben A (3/0), B (0/5), C (5/2) gegeben. Zeichnen Sie das Dreieck in einem rechtwinkeligen Koordinatensystem. Messen Sie die Winkel. Konstruieren Sie die Streckensymmetralen der Dreiecksseiten. Hinweis: Eine Streckensymmetrale (Mittelsenkrechte) ist eine senkrechte Gerade durch den Mittelpunkt der Seite. Woran können Sie erkennen, dass das Dreieck ein gleichschenkeliges Dreieck ist?
Lösung
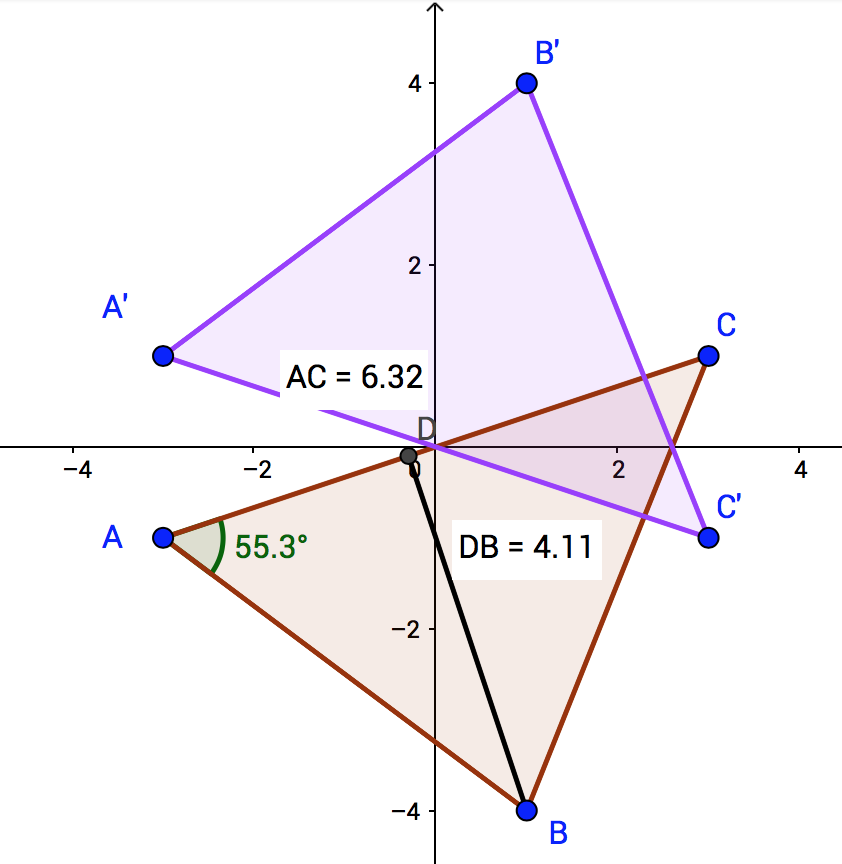
Zeichnen Sie das Dreieck A(–3|–1), B(1|–4), C(3|1) in ein Koordinatensystem ein. Berechnen Sie den Flächeninhalt des Dreiecks ABC. Messen Sie den Winkel ab, und notieren Sie seinen Wert. Spiegeln Sie das Dreieck an der x-Achse. Hinweis: Spiegeln bedeutet, dass Sie die kürzeste Entfernung eines Punktes zur Spiegelachse auf die andere Seite übertragen. Dazu wird eine Senkrechte auf die Spiegelachse durch den Punkt errichtet.
Lösung
Das soll fürs Erste genug sein. Wir nähern uns dem Ende des Sommerkurses. Ein bisschen was gibt’s noch zu tun. Kommen Sie wieder, machen Sie weiter, bleiben Sie dran – bald schon im 18. Kapitel.
Korrekturen: Maria Fatoba
Fehler gefunden? Bitte schicken Sie ein E-Mail an fehler@phyx.at. Vielen Dank!



